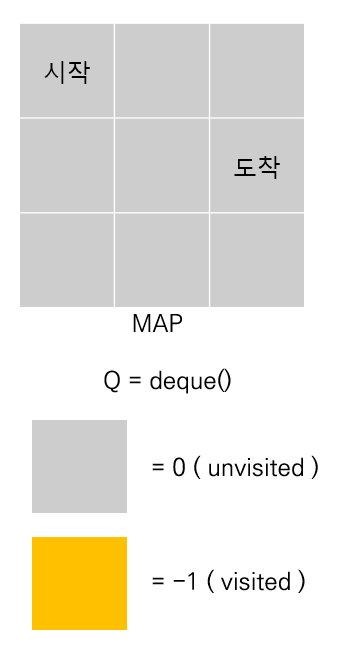
"시작점 (0, 0) 도착점 (1, 2)일 때, 2차원 배열 (3X3)에서 시작점으로부터 도착점까지의 최단거리를 찾아라"는 문제를 푸는 과정입니다.
우선 2차원 배열과 queue를 선언합니다.

본인이 설정해 둔 move에 맞게, 값을 더해가며 현재 위치에서 북, 동, 남, 서 순으로 순회하며 다음 갈 위치를 계산합니다.
아래 그림은 현재 위치(시작 위치)에서 북, 동쪽을 탐색하는 과정입니다.

이런식으로 북, 동, 남, 서를 위치마다 한번씩 다 탐색하게 됩니다. (아래 그림)
nx,ny가 MAP의 범위를 초과했거나, 이미 방문했던 노드인 경우에는 생략합니다.

위 그림처럼 (0,0)위치에서 다 순회한 이후에는 다시 현재 queue의 맨 앞 원소를 pop하여 (0,1)에서 북, 동, 서, 남 을 순회합니다.
아래쪽 그림처럼 (0,0)의 북,동,서,남 ==> (0,1)의 북,동,서,남 ==> (1,0)의 북,동,서,남 ==> (0,2)의 북,동,서,남 ==> ... => 도착지점을 만날때까지 계속해서 탐색합니다.
여기까지 bfs의 탐색 동작과정입니다. 최단거리는 위 동작과정에 한가지 동작만 추가해주면 됩니다.
bfs에서 시작점으로부터 nx,ny까지의 최단거리는 x,y까지의 최단거리 + 1의 거리입니다. 항상 현재 위치(x,y) 에서 1칸씩 nx,ny를 탐색하기 때문입니다. 따라서, queue에 현재 위치에서의 최단거리 정보를 같이 저장해주면, 간단하게 구할 수 있습니다.
아래 사진에서 보면, 이전까지는 queue에 (x,y)만을 저장했다면, 이제는 최단거리 정보를 위해 queue에 (x,y,현재위치(x,y)까지의 최단거리)를 저장합니다. 따라서, (0,0)에서부터 (2,1)까지의 최단거리가 3이 됩니다.


이를 코드로 나타내면
from collections import deque
N = 3 # MAP 크기
MAP = [[0 for _ in range(N)] for _ in range(N)]
visited = [[0 for _ in range(N)] for _ in range(N)]
start_row, start_column = 0,0 # 시작 행,열 인덱스
target_row, target_column = 1, 2 # 도착 행, 열 인덱스
move = {(-1,0),(0,1),(1,0),(0,-1)} #북동남서
cnt = 0
q = deque()
q.append((start_row, start_column, cnt))
visited[start_row][start_column] = 1
while q:
cur_row, cur_column, cnt = q.popleft()
if cur_row == target_row and cur_column == target_column:
break
for next_r, next_c in move:
next_row = cur_row + next_r
next_column = cur_column + next_c
if 0<=next_row<N and 0<=next_column<N \
and visited[next_row][next_column] != 1:
q.append((next_row, next_column, cnt + 1))
visited[next_row][next_column] = 1
print(cnt)