2019 cvpr에 나온 최초의 arbitrary scale image super-resolution 연구,,
수식 로딩 안 된 경우 새로고침 한번,,
Abstract
deep convolutional neural networks를 활용한 super-resolution(SR) 연구과 뛰어난 성능을 보이고 있다. 그러나, arbitrary scale에 대한 SR 연구는 오랫동안 외면받았다. 기존의 많은 연구자들은 다른 scale factor를 가지는 SR를 독립적인 task로 다루었다. 기존에는 각각에 scale에 맞게 모델을 학습시켜서 비효율적이고, 정수배의 scale facotr에 대한 문제만 고려했다. 본 연구에서 우리는 arbitrary scale factor(실수배의 scale factor를 포함) SR를 단 하나의 모델로 수행하는, 최초의 novel method인 Meta-SR을 제안한다. Meta-SR에서는 traditional upscale module을 Meta-Upscale Module로 대체한다. arbitrary scale factor에 대해, Meta-Upscale Module은 scale factor를 input으로 받아 upscale filter의 weight을 동적으로 예측하고, 이 weight으로 arbitrary size의 이미지를 SR 한다. 어떤 low-resolution image가 있건, 이 Meta-SR은 하나의 모델을 사용해서 연속적으로 arbitrary scale factor로 이미지를 zoom 할 수 있다.
Introduction
실생활에서, Low-resolution(저화질, LR) 이미지를 사용자가 원하는 scale만큼 확대(zoom)하는 것은 흔하고 필수적인 일이다. 일반적인 이미지 뷰어에서는 사용자가 이미지의 디테일을 확인하기 위해서 마우스 휠을 해서 이미지를 zoom 하여 arbitrary scale로 확대할 수 있다. 이러한 상황에서 customize 되는 scale factor는 어떠한 양수(고정된 정수 X)라도 될 수 있다. 그래서, arbitrary scale문제를 해결하는 것은 Single Image Super-resolution(SISR)를 더 실용적으로 활용하기 위해 중요하다. 각각의 양의 scale factor마다 모델을 훈련시키고 저장하는 것은 불가능하고 비효율적이어서 하나의 모델로 arbitrary scale factor의 SR을 풀 수 있는지가 중요한 부분이다.
그러나, 우리가 알다싶이 대다수의 기존 SISR 방법들은 고정된 배수 (X2, X3, X4)에 대해서만 SR를 고려한다. SOTA(2019년 기준) 성능을 보이는 SISR 모델들은 네트워크 끝에서 sub-pixel convolution으로 원하는 정수배 스케일에 맞게 feature map을 zoom 하고 각각의 upscale module은 고정된 정수배 스케일에 대해서만 이미지를 확대할 수 있다. '고정'된 '정수'배에만 사용할 수 있다는 단점 때문에 기존 SISR은 실생활에 적용하는데 한계가 있다. input image를 적절하게 확대하면 실수배율에 대한 SR을 구현할 수는 있지만, 반복적인 계산과 upscaled input으로 인해 이런 방법들은 매우 시간이 많이 소요되며 실용적으로 사용하기 어렵다.
이런 단점들을 해결하고 SISR을 더 실용적으로 사용하기 위해서, 하나의 모델을 사용하여 arbitrary scale SR을 수행할 수 있는 이상적인 방법이 필요하다. 하나의 모델로 arbitrary scale SR 하는 문제를 풀려면, 각각의 scale factor에 대한 upscale filter의 weight 그룹이 필요하다. 본 논문에서는, meta-learning에 영감을 받아, 각각의 scale factor에 대해 동적으로 필터의 weight을 예측하는 신경망을 제안한다. 더이상 각각의 scale factor에 대한 weight을 저장할 필요가 없어지고, 훨씬 효율적이다.
본 논문에서는 이 방법은 Meta-SR이라고 명명한다. Meta-SR에는 feature Learning Module과 Meta-Upscale Module이 있다. Meta-Upscale Module은 일반적인 upscale module을 대체한다. SR이 끝난 생성된 High Resolution(HR) 이미지에서 각각의 픽셀 $(i, j)$ 를 Low-resolution(LR) 이미지에 scale factor $r$을 기반으로 투영한다(Location Projection). Meta-Upscale Module은 이 좌표와 스케일과 연관된 벡터를 input으로 받고 filter의 weight을 예측한다(Weight Prediction). 생성된 SR 이미지에서 각각의 좌표 $(i, j)$에 대해, LR 이미지의 해당 투영 좌표$(i', j')$에서의 feature와 filter weight 사이에 convolution 연산이 수행되어 SR이미지의 픽셀 $(i, j)$의 값을 생성한다(Feature mapping). 이 Meta-Upscale Module은 스케일, 좌표와 연관된 벡터를 input으로 받아 convolution filter의 weight을 동적으로 예측할 수 있다. 이 방법으로, Meta-Upscale Module은 feature map을 하나의 모델에서 arbitrary scale에 대해 확대할 수 있게 된다. 이 방법은 기존 upscale을 모듈을 대체하여 기존 SR 모델들에 적용할 수 있다.
본 논문에서는 실험을 통해 다음 결과를 보여준다.
1) meta-SR이 정수배 SR 모델과 비등한 성능을 보인다.
2) 그냥 feature map을 확장하여 보간하는 것보다 좋은 성능을 보인다.
3) 빠르다. (이 포스팅에선 관련 내용 정리 안함)
Method
3.1 Meta-Upscale Formulation
$I^{SR}$ : SR 된 이미지
$I^{LR}$ : LR 이미지
$I^{HR}$ : HR 이미지(GT)
$F^{LR}$ : Feature Learning Module에서 추출된 feature
$r$ : scale factor(배율)
본 연구에서는 SR 이미지의 각 픽셀 $(i, j)$가 LR이미지의 $(i', j')$의 피쳐와 그와 연관된 필터의 가중치로부터 결정된다고 본다. 이 관점에서, upscale module은 $I^{SR}$과 $F^{LR}$의 mapping function으로 볼 수 있다. 처음에 upscale module은 $(i, j)$을 $(i', j')$로 mapping 한다. 그리고 upscale module은 LR 이미지의 $(i', j')$의 feature를 mapping 하기 위해 특정한 filter가 필요하며 이를 통해 SR 이미지의 픽셀 $(i, j)$을 생성한다. 이 과정을 아래의 식으로 나타낼 수 있다.
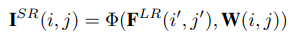
$I^{SR}(i, j)$ : SR 이미지의 픽셀 $(i, j)$
$F^{LR}(i', j')$ : LR 이미지의 픽셀 $(i', j')$의 feature
$W(i, j)$ : $(i, j)$에 대한 필터의 가중치
$\Phi(.)$ : 픽셀 값을 계산하기 위한 mapping function
SR 이미지의 각각의 픽셀은 filter와 연관되어 있다. 다른 scale factor에 마다 filter의 수와 filter weight은 다르다. 하나의 모델로 임의의 스케일에 대한 SR을 풀기 위해, 본 연구에서는 Meta-Upscale Module에서 SR 이미지의 한 픽셀 $(i, j)$에 대한 가중치 $W(i, j)$를 배율(scale factor)과 좌표 정보를 기반으로 동적으로 예측한다.
Meta-Upscale Module에서는 세 가지 중요한 기능 Location Projection, Weight Prediction, Feature Mapping이 있다. 그림 2에서 볼 수 있듯, Location Projection은 pixel을 LR 이미지로 투영한다. Weight Prediction Module은 SR 이미지의 각 픽셀에 대한 filter의 weight을 예측한다. Feature Mapping function 은 LR이미지의 feature를 예측된 weight와 함께 SR 이미지로 mapping 하여 각 픽셀값을 계산한다.
Location Projection
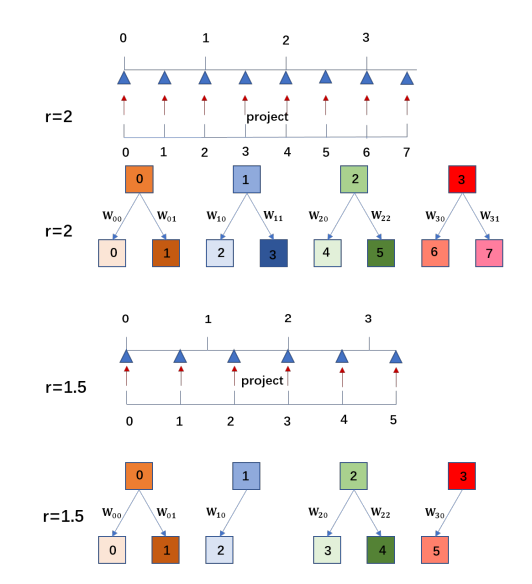
location projection은 SR 이미지의 픽셀 $(i, j)$에 대응하는 LR 이미지의 $(i', j')$를 찾는 것이다. LR 이미지의 $(i', j')$와 SR 이미지의 픽셀 $(i, j)$를 아래와 같이 mapping 했다.
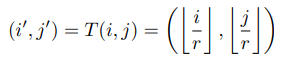
Location Projection은 arbitrary scale factor에 대해 feature map을 upscale 할 수 있는 *variable fractional stride의 일종으로 볼 수 있다.
그림 2에서 볼 수 있듯이, 만약 scale factor가 2이면, 각 픽셀 $(i', j')$은 두 개의 지점을 결정한다. 그러나 실수배의 경우, 예를 들어 scale factor r = 1.5 이면, 몇 개의 픽셀은 두 픽셀을 결정하지만 몇 개의 픽셀은 한 개의 픽셀만 결정한다. SR 이미지의 각 픽셀 $(i, j)$에 대해서, LR 이미지의 특정한 $(i', j')$을 찾을 수 있고 이 두 픽셀이 가장 관련이 있는 것으로 간주한다.
* variable fractional stride
일반적인 convolution 연산에서는 stride가 고정되어 있다. variable fractional stride convolution의 경우 stride의 크기를 다양하게 하여 feature에서 더 다양하고 미세한 패턴을 학습하는 convolution이다.
Weight Prediction
일반적인 upscale module에서, 각 scale factor에 대해 필터의 수는 미리 고정되어 있고, training dataset에 대해 $W$를 학습한다. 일반적인 upscale module과 다르게, 이 Meta-Upscale Module은 필터의 가중치를 예측하는 신경망을 사용한다. weight prediction 과정을 다음과 같이 정리할 수 있다.
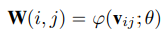
$W(i, j)$ : $(i, j)$에 대한 필터의 가중치
$v_{ij}$ : $(i, j)$와 연관된 벡터
$\varphi(.)$ : $v_{ij}$를 input으로 받는 weight prediction 신경망
$\theta$ : weight prediction 신경망의 파라미터
픽셀 $(i, j)$에 대한 모델 $\varphi(.)$의 input으로 적절한 선택은 $(i', j')$로 가는 relative offset이다. $v_{ij}$는 아래와 같이 정리할 수 있다.
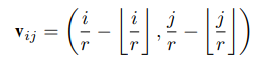
여러 scale factor에 대해 함께 train 하기 위해서, 다른 scale factor에 대해 weight을 미분하기 위해 $v_{ij}$에 scla factor를 넣는 것이 좋다. 예를 들어, 만약 2배, 4배로 upscale한걸 각각 $I_2^{SR}$ , $I_4^{SR}$라고 한다. $I_2^{SR}$에 대한 픽셀 $(i, j)$는 $I_4^{SR}$에 대한 픽셀 $(2i,2j)$와 같은 projection coordinate와 같은 filter weight를 가진다. 이건 $I_2^{SR}$ 가 $I_4^{SR}$ 의 subimage임을 의미하게 된다. 성능에 제한이 될 수 있으므로 $v_{ij}$를 아래와 같이 재정의 했다.
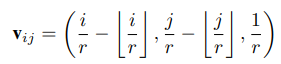
Feature Mapping
지금까지 과정에서 $F^{LR}$로부터 LR 이미지의 픽셀 $(i', j')$의 피쳐를 추출했다. 그리고 weight prediction 신경망으로 filter의 weight을 예측했다. 마지막으로는 feature를 SR이미지의 픽셀값으로 mapping 해야 한다. Feature Mapping function $\Phi(.)$로는 matrix product를 선택했다.

이 세 가지 function을 가지는 Meta-Upscale Module은 다음과 같이 정리된다.

3.2 Architecture Details of Meta-SR
앞서 명시했든 Meta-SR은 Feature Learning Module과 Meta-Upscale 두 가지 파트로 이루어져 있다. 이중 Feature Learning Module로는 기존 SOTA SISR 모델 구조를 사용할 수 있다. 기존 SOTA SISR 모델들의 upscale을 단순히 Meta-Upscale Module로 대체하여 Meta-SR을 구성할 수 있다.
Experiments
L1 loss를 사용함.
4.3. Single Model For Arbitrary Scale Factor
단일모델로 arbitrary scale에 집중한 이전 접근이 없기 때문에 본 논문에서는 몇 개의 basline을 디자인했다. Meta-SR와 이 baseline들을 비교하여 Meta-SR의 우수성을 증명했다.
LR이미지를 (1,4]의 scale로 zoom 한다고 가정하자. 신경망으로 upscale 하기 전에 bicubic interpolation으로 upscale 했고, 이걸 첫 번째 baseline으로 삼았다(bicubic baseline).두 번째 baseline은 먼저 LR 이미지를 r배 확대하고, CNN-based SR 모델(EDSR or RDN)에 넣어 HR이미지를 생성한다. 이 방법은 시간이 많이 소요되며 실용적으로 사용하기 어렵다. 세 번째 baseline은 생성된 HR을 downscale 한다. k배 upscale 하는 신경망 G가 있다고 가정하자. 우리는 LR 이미지를 신경망에 넣어 k배의 HR이미지를 생성할 수 있다. 그리고 다시 생성한 HR 이미지를 $\frac {r}{k}$배 downscale 하여 LR을 $r$배 upscale 한 결과를 예측한다. $k=2$일 때가 세 번째 baseline, $k=4$일 때가 네 번째 baseline이다. 만약 $r> k$이면 모델에 입력하기 전에 LR 이미지를 확대한다.
Weight Prediction과 Location Projection의 우수성을 증명하기 위해서 우리는 다섯 번째 baseline(BicuConv)를 디자인했다. 마지막 feature map을 interpolation 하고 모든 scale factor에 대해 고정된 convolution featuremap을 사용했다. ( 마지막 upscale module에서 convolution의 weight은 고정하고, feature map만 스케일에 따라 보간. weight predition 과정 X) 여섯 번째 baseline(Meta-BiCu)에서는 feature map을 바로 interpolation 했다. 여섯 번째 방법에서는 weight prediction 신경망을 사용하여 각 scale에 대한 convolution filter의 weight을 예측했다.
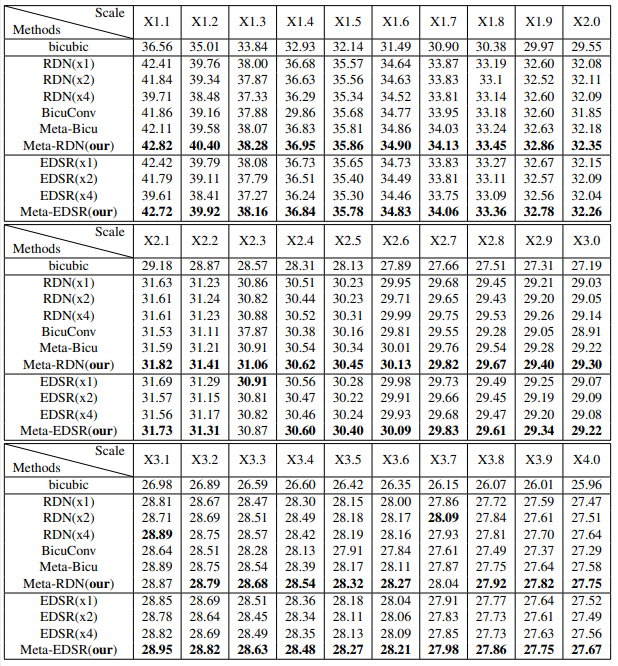
첫 번째 베이스라인의 결과는 디테일이 잘 보존되지 않고 성능이 제한적이다.
두 번째 베이스라인은 large-scale factor에 대해 성능이 낮고 upscaling 하는데 시간이 많이 소요된다.
네 번째 베이스라인의 경우 scale이 1에 가까워질수록 meta-SR과 성능 차이가 많이 난다.
여섯 번째 베이스라인과 본 논문이 제안한 meta-SR의 경우 weight prediction 기능이 있기 때문에 각 scale에 대한 최적의 filter weight를 학습할 수 있었고, 다섯 번째 베이스라인은 모든 scale에 대해 같은 filter weight을 공유한다. 그 결과, Meta-Bicu가 BicuConv보다 유의미하게 우수하며, 이는 weight prediction module의 우수성을 보여준다. feature map interpolation에서는 scale이 클수록 FOV(시야)가 작아진다. 하지만 Meta-SR에서는 모든 scale이 동일한 FOV를 가져서 Meta-RDN가 다른 baseline들에 비해 거의 모든 scale에 대해서 성능이 좋다.
Conclusion
Meta-Upscale이라는 novel upscale module제안한다. 동적으로 filter의 weight을 계산해서 단일 모델로 arbitrary scale SISR을 가능하게 한다.
